近日,数学学院姬超教授与其博士研究生何镇涛在非线性偏微分方程领域取得重要研究进展。其合作论文《Normalized solutions of nonlinear Dirac equations on noncompact metric graphs with localized nonlinearities》发表于数学领域国际权威期刊Journal de Mathématiques Pures et Appliquées(2026年第206卷)。该期刊创刊于1836年,由法国著名数学家Joseph Liouville创办,是现存历史第二悠久的国际数学期刊,在数学界享有崇高的学术声誉。

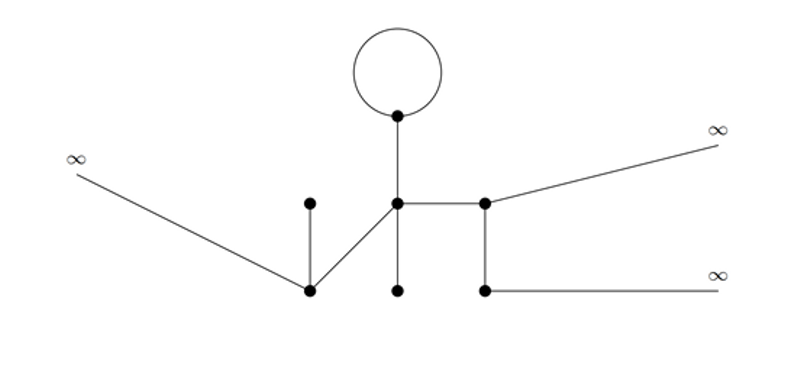
图片说明:带有限条边和非空紧核的非紧度量图
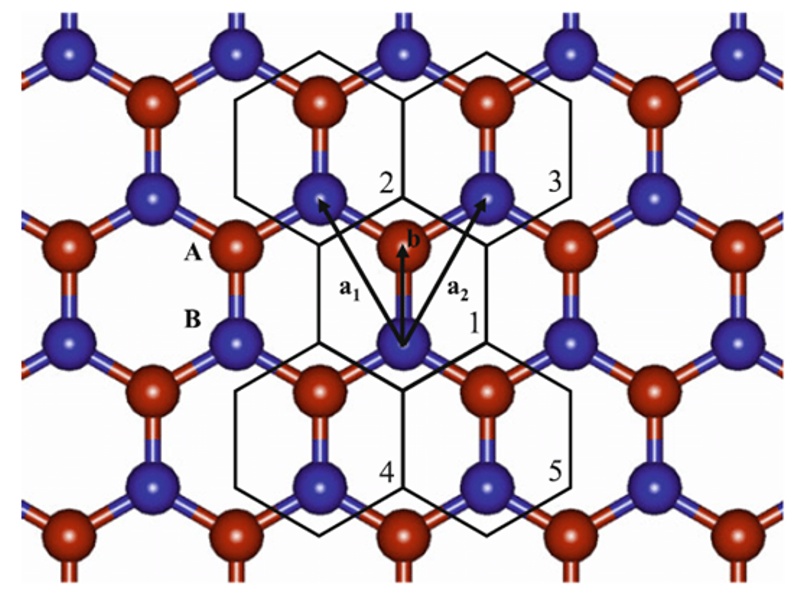
图片说明:石墨烯蜂窝晶格
度量图上的非线性Dirac方程研究为量子网络和低维纳米材料的应用提供了新的数学模型。该方程不仅能够描述具有复杂拓扑结构的粒子动力学,还能模拟例如石墨烯等材料中电子的行为。尽管目前在非线性Schrödinger方程方面已有诸多成果,但针对非线性Dirac方程的正规化解研究仍是一片空白。该论文首次系统地研究了带局部非线性的非紧度量图上的非线性Dirac方程正规化解的存在性。作者利用扰动方法,通过构造特殊的测试函数,克服了度量图上缺乏傅里叶变换以及能量泛函具有强不定性等本质困难,证明了质量次临界情形下正的非线性项系数充分小时正规化解的存在性。此外,利用图论与算子谱理论,作者还进一步揭示了度量图的几何结构对正规化解存在性的深刻影响,主要是给出了质量次临界情形下对于任意非零非线性项系数正规化解存在的充分条件和质量超临界情形下正规化解存在的充分条件。该工作不仅填补了现有文献在度量图上非线性Dirac方程正规化解研究方面的空白,也为理解相对论粒子在度量图结构中的动力学行为提供了新的数学理论支撑。
该工作第一作者为博士生何镇涛,通讯作者为姬超教授,该工作得到了国家自然科学基金的资助。
原文链接:https://www.sciencedirect.com/science/article/pii/S0021782425001813






